# -*- coding: utf-8 -*-
"""Q-Learning-FrozenLake_v3.ipynb
Automatically generated by Colaboratory.
Original file is located at
https://colab.research.google.com/drive/1tuAm79lVLp6s6_eCNW3DyH4ohTpWI3sQ
# Q* Learning - FrozenLake
In this Notebook, we'll implement an agent that plays FrozenLake.
The goal of this game is to go from the starting state (S) to the goal state (G) by walking only on frozen tiles (F) and avoid holes (H).However, the ice is slippery, so you won't always move in the direction you intend (stochastic environment)
Reference: code adapted from
https://github.com/simoninithomas/Deep_reinforcement_learning_Course/blob/master/Q%20learning/FrozenLake/Q%20Learning%20with%20FrozenLake.ipynb
"""
import numpy as np
import gym #to load the FrozenLake Environment
import random
import matplotlib.pyplot as plt
env = gym.make("FrozenLake-v0")#this command creates the FrozenLake environment using the gym library of environments
#is_slippery=False
env.reward_range
env.metadata
env.spec
env.action_space.contains(2)
#env.desc
env.reset()
"""## Step 2: Create the Q-table and initialize it """
action_size = env.action_space.n#how many actions there are
state_size = env.observation_space.n#how many states there are
qtable = np.zeros((state_size, action_size))
print(qtable)
"""## Set the hyperparameters"""
total_episodes = 50 # Total episodes
learning_rate = 0.8 # Learning rate
max_steps = 99 # Max steps per episode
gamma_rate = 0.95 # Discounting rate
# Exploration parameters
epsilon = 1.0 # Exploration rate
max_epsilon = 1.0 # Exploration probability at start
min_epsilon = 0.01 # Minimum exploration probability
decay_rate = 0.005 # Exponential decay rate for exploration prob
"""## Step 4: The Q learning algorithm
- Now we implement the Q learning algorithm:
"""
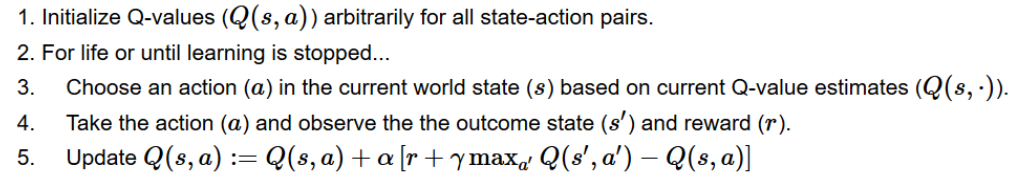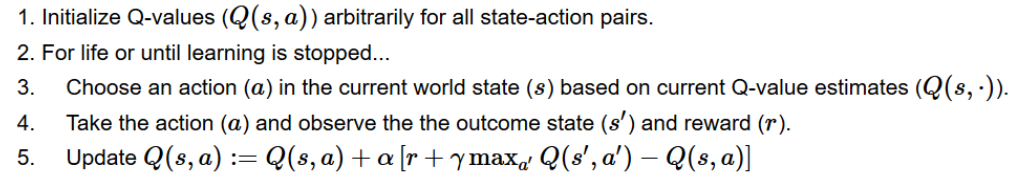# List of rewards
rewards = []
for episode in range(total_episodes):
# Reset the environment
state = env.reset()
step = 0
done = False
total_rewards = 0
for step in range(max_steps):
# epsilon-greedy strategy
exploration_or_exploitation = random.uniform(0, 1)
## If this number > greater than epsilon --> exploitation (taking the biggest Q value for this state)
if exploration_or_exploitation > epsilon:
action = np.argmax(qtable[state,:])
# Else doing a random choice --> exploration
else:
action = env.action_space.sample()
# Take the action (a) and observe the outcome state(s') and reward (r)
new_state, reward, done, info = env.step(action)
# Update Q(s,a):= Q(s,a) + lr [R(s,a) + gamma * max Q(s',a') - Q(s,a)]
# qtable[new_state,:] : all the actions we can take from new state
qtable[state, action] = qtable[state, action] + learning_rate * (reward + gamma_rate * np.max(qtable[new_state, :]) - qtable[state, action])
total_rewards += reward
# Our new state is state
state = new_state
# If done (if we're dead) : finish episode
if done == True:
break
# Schedule to reduce epsilon
epsilon = min_epsilon + (max_epsilon - min_epsilon)*np.exp(-decay_rate*episode)
rewards.append(total_rewards)
print ("Score over time: " + str(sum(rewards)/total_episodes))
print(qtable)
# visualisation de la table Q pour FrozenLake
def plotQ(q_table,env):
MAP=env.desc
map_size=MAP.shape[0]
best_value = np.max(q_table, axis = 1).reshape((map_size,map_size))
best_policy = np.argmax(q_table, axis = 1).reshape((map_size,map_size))
fig, ax = plt.subplots()
im = ax.imshow(best_value,cmap=plt.cm.Wistia)#Pastel1, spring, autumn
arrow_list=['<','v','>','^']
for i in range(best_value.shape[0]):
for j in range(best_value.shape[1]):
if MAP[i][j].decode('utf-8') in 'GH':#terminal states
arrow = MAP[i][j].decode('utf-8')
else :
arrow=arrow_list[best_policy[i, j]]
if MAP[i][j].decode('utf-8') in 'S':
arrow = 'S ' + arrow
text = ax.text(j, i, arrow, ha = "center", va = "center",
color = "black")
text2 = ax.text(j, i+0.2, str(np.round(best_value[i,j],2)),
ha = "center", va = "center",color = "blue")
cbar = ax.figure.colorbar(im, ax = ax)
plt.axis('off')
fig.tight_layout()
plt.show()
plotQ(qtable,env)
#print(qtable)
#np.max(qtable, axis = 1).reshape((4,4))
#look at https://gsverhoeven.github.io/post/frozenlake-qlearning-convergence/ for the optimal value function
"""## Step 5: Use the Q-table to play FrozenLake
- After 10 000 episodes, our Q-table can be used as a "cheatsheet" to play FrozenLake"
- By running this cell you can see our agent playing FrozenLake.
"""
env.reset()
rewards = []
total_test_episodes=10
for episode in range(total_test_episodes):
state = env.reset()
step = 0
done = False
total_rewards = 0
print("****************************************************")
print("EPISODE ", episode)
for step in range(max_steps):
# Take the action (index) that have the maximum expected future reward given that state
action = np.argmax(qtable[state,:])
#env.render()
new_state, reward, done, info = env.step(action)
total_rewards +=reward
if done:
# Here, we decide to only print the last state (to see if our agent is on the goal or fall into an hole)
env.render()
# We print the number of step it took.
print("Number of steps", step)
break
state = new_state
rewards.append(total_rewards)
print ("Score over time: " + str(sum(rewards)/total_test_episodes))
env.close()
"""
```
# Ce texte est au format code
```
##Questions
- is the obtained value function optimal ?
- is the obtained policy optimal ?
- when $\gamma$ goes to $1.0$ do the policy changes ?
- change the total number of training episodes
"""