| Application domain | topics | Math tools used |
|---|---|---|
| Artificial Intelligence / Machine learning, Neural networks (since 2000) | Generative models : GAN, VAE, stochastic optimization and applications | deep learning, neural networks, statistical learning, GAN, VAE, genetic algorithms |
| Medecine (since 2003) | Epidemiology and epidemic propagation: mathematical models, simulations, reinfection. VACCINATION: models and applications Immunology and inflammation: intra-host mathematical models | numerical simulations; parameter estimation, game theory; Mean Field Games; control theory; optimization; mass transportation |
| Numerical statistics (since 2004) | measure compression, etc. | vector quantification, clustering, measure compression |
| Numerical analysis and computer simulations (since 1998) | efficient discretizations, parallel in time algorithms, error estimation | reduced basis; parareal algorithm; a posteriori error analysis |
| Finance (since 2005) | local volatility, FOREX options, corporate loand | numerical optimization; adjoint state, stochastic calculus; CIR model; jump dynamics |
| quantum physics and chemistry (since 1998) | Quantum control Inversion and discimination, Ab initio computations | control theory, optimization, stochastic learning, numerical optimization |
Deep Generative networks / generative AI
The generative models as GAN/ VAE and derived are the most efficient amongst the tools used today to create new objects from a database of old ones. I advocate the use of specific statistical distances, such as the energy distance, Radon-Sobolev distances etc., see related papers for additional information.
One particular topic is related to the notion of quantization, that resumes large sets of objects into a shorter description with only few objects. This can be used in many ways: conditional quantization to recover e.g. missing parts of an image or to complete a text (à la chatGPT), diversity sampling to generate objects that do not ressemble to old ones, etc.
Multi-agent and uncertainties: Mean Field Games
We explore in this topic the behavior of a large crowd of people that have to take decisions in an uncertain environment.
The mathematical models and methods witnessed important developpement since the introduction of the Mean Field Games theory (by Lasry ˇ& Lions and indepently by Cuang& Caines & Malhame. In this formulation each individual takes decision according to what the sum of all other people is already doing. An individual cannot influence the others BUT his actions are influenced by the aggregate effects of all decisions of others.
Several works appear to use these techniques in the field of social sciences. However many questions remain. We explore several applications: in economics (work with A. Lachapelle and J. Salomon and R. Aid) and in medecine/ vaccination (see dedicated topic HERE).
Initial references (see on google scholar recent ones):
Vaccination : see topic below.
Computation of mean field equilibria in economics (A Lachapelle, J Salomon, G Turinici) Mathematical Models and Methods in Applied Sciences 20 (04), 567-588 | PDF: <hal-00346214v2>
Vaccination
Vaccination coverage in developed countries weakens significantly over concerns regarding the side-effects of the vaccines. As a consequence the non-compulsory vaccination programs have to take into account the willingness of the people to vaccinate (and not only the general, societal, interest to do so). This perspective is very recent and has only been addressed in research works in the last 10-15 years.
The problem of finding the optimal vaccination as response to an ongoing epidemic has been traditionally addressed in the framework of optimal control theory. These tools give the best vaccination policy optimizing the overall, societal outcome.However adherence to the prescribed vaccination program is not always optimal at the individual level. To address this situation, new models, coming from the game theory have been introduced. The vaccination is therefore seen not as a result of centralized recommandations but as an equilibrium between individual and the society.
Indeed, recent debates concerning the innocuity of vaccines with respect to the risk of the epidemic itself lead to vaccination campaign failures. We analyze, in a SIR model, whether individuals driven by self interest can reach an equilibrium with the society. We show, in a Mean Field Games context, that an equilibrium exists and discuss the « price of anarchy ». Finally, we apply the theory to the 2009-2010 Influenza A (H1N1) vaccination campaign in France.
 |
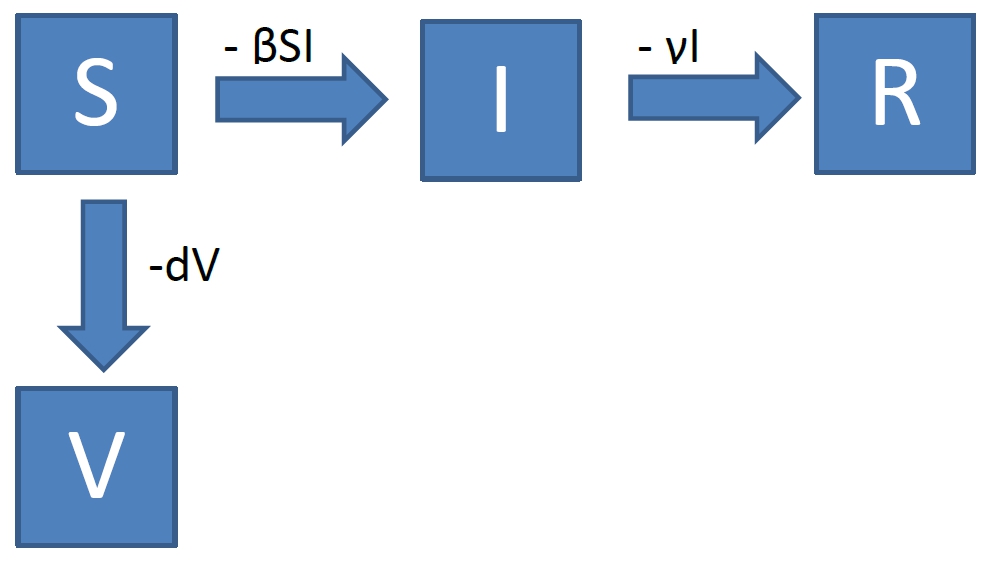| The SIR model (with vacciation) used to predic epidemic propagation. |
 |
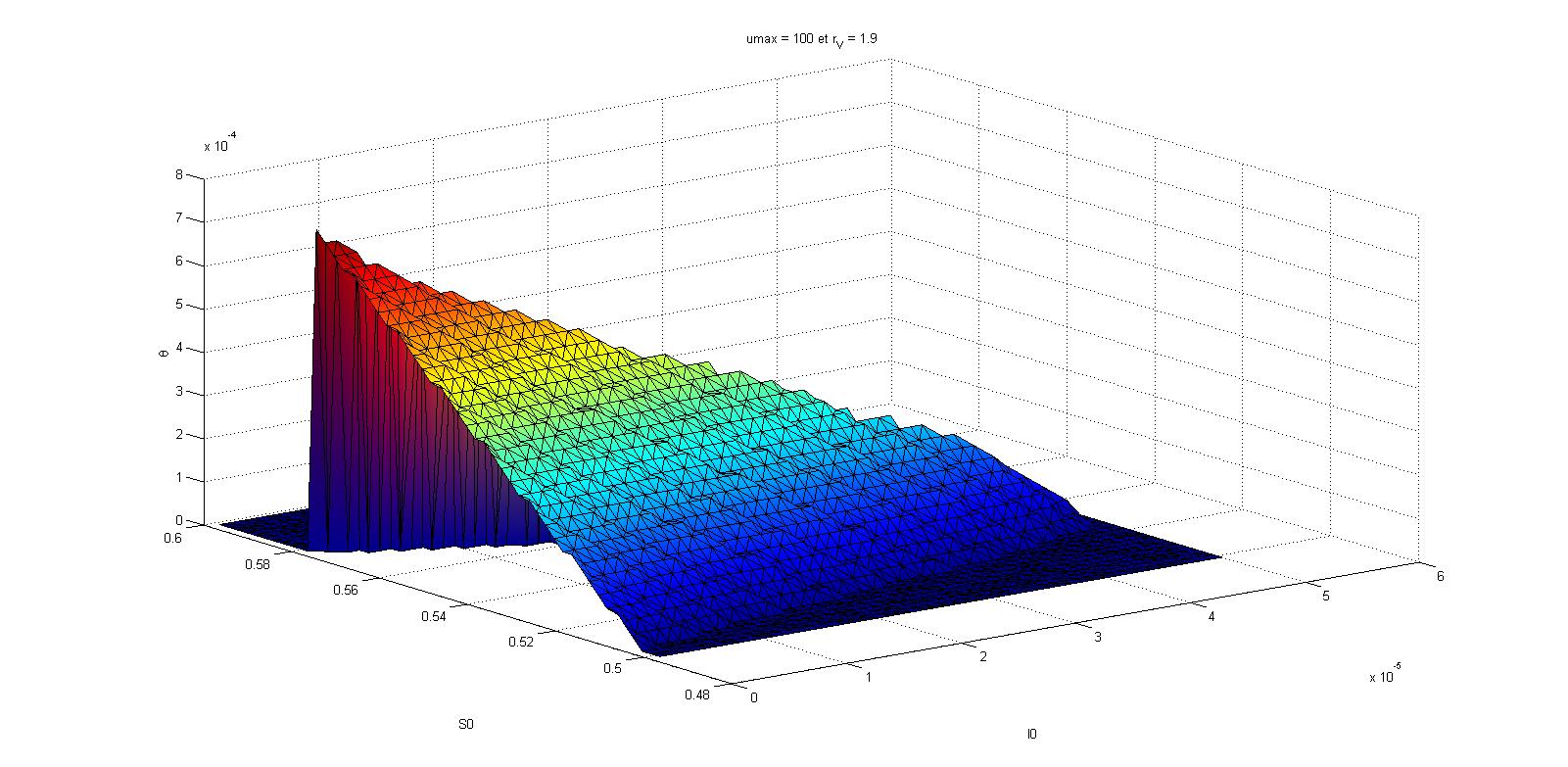| The prediction of vaccination time that balance individual and societal interests. |
Initial references (cf. to google scholar for recent ones) :
General vaccination reference (not at the individual level) Global optimal vaccination in the SIR model: Properties of the value function and application to cost-effectiveness analysis (L Laguzet, G Turinici) Mathematical biosciences 263, 180-197 PDF: <hal-00966622v2>
Dynamical discrimination of molecules
Similar molecules often may be characterized as sharing common chemical structures made up of the same atomic components. Such molecules are expected to have related Hamiltonians, and thus similar chemical and physical properties. Examples range from simple isotopic variants of diatomics (e.g., 79Br2, 81Br2) and isomers (e.g., cis- and trans-1,2-dichloroethylene) to highly complex molecules including those of biological relevance. A common need is to analyze or separate one molecular species in the presence of possibly many other similar agents. This problem often demands rapid, sensitive, and dependable identification or purification measures. Traditional approaches mainly focus on exploiting the subtle differences in the microscopic properties, or macroscopic properties; these methods have seen wide applications, but they may all be characterized as static or one-dimensional with their capabilities being pushed to the limit. To enhance the ability to distinguish molecules, a new paradigm is proposed aiming for optimal discrimination by actively amplifying the seemingly subtle differences between similar molecules. The proposed optimal dynamic discrimination (ODD) approach exploits the richness of quantum molecular dynamics. Although the dynamics of similar quantum systems are governed by related Hamiltonians, each species could evolve in a distinct fashion under the same properly tailored external control, e.g. a laser field. The wave packets of the similar molecules in the system are excited by a common laser pulse, which is tailored with the goal of inducing signals (possibly detected with another common laser pulse) from only one species, while suppressing signals from all the others. Optimal control techniques are potentially ideal tools for implementing ODD, as the underlying closed loop learning control process inherently operates based on achieving discrimination between one dynamical process versus another.
References: Optimal dynamic discrimination of similar molecules through quantum learning control (B Li, G Turinici, V Ramakrishna, H Rabitz) The Journal of Physical Chemistry B 106 (33), 8125-8131
 |
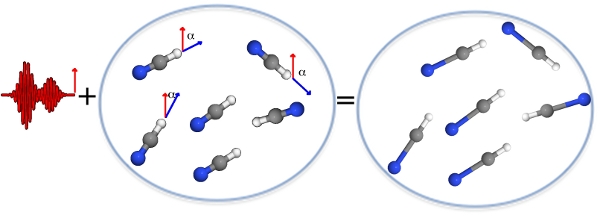| An optimized laser pulse that allows to control the lenght of a chemical bond (or to create another bonds). copyright Gabriel Turinici 2010 |
Algorithms for experimental realization of quantum control
Experimental realization of quantum control is done in practice through the online minimization of a cost functional that is computed by measurements; the minimization algorithm used is most often a derivative of Genetic Algorithms or Evolutionary Strategy paradigm. The understanding of how this algorithm manage to find the good solutions and its practical implications at the goal of this part of my research Controllability in bilinear quantum chemistry models
The control of quantum phenomena has been demonstrated on a variety of experimental setings. However, fundamental questions remains still unanswered in this field such as the good notions of controllability of the infinite-dimensional equations and also the search for the easy implementable criterions to assess this controllability property. Some results may be adapted from the already obtained experience with the finite-dimensional setings. Monotonic algorithms for quantum optimal control
Laser control of complex molecular and solid-state systems is becoming feasible, especially since the introduction of closed loop laboratory learning techniques and their successful implementation. However, at the level of the numerical simulations, much work is still to be done in order to bring the size of the systems that can be treated accurately to practical dimensions. Of course, using a good algorithm to solve the quantum control critical point equations is very important to the reduction of the overall cost; some of the most used algorithms nowadays falls within the class of « monotonically convergent » algorithms that are guaranteed to improve the performance (measured through a cost functional) a each step. My work in this area aims at describing new classes of monotonic algorithms and also at further studying their convergence properties.
Most cited references:
Quantum wavefunction controllability G Turinici, H Rabitz Chemical Physics 267 (1), 1-9
New formulations of monotonically convergent quantum control algorithms Y Maday, G Turinici, The Journal of Chemical Physics 118 (18), 8191-8196