Statistics and dynamics of financial derivatives, M2 ISF App, 2020+

Teacher: Gabriel TURINICI

Content

• classical portfolio mangement under historical probability measure: optimal portfolio, arbitrage, APT, beta
• Financial derivatives valuation and risk neutral probability measure
• Volatility trading
• Portfolio insurance: stop-loss, options, CPPI, Constant-Mix
• Hidden or exotic options: EFT, shorts
• Deep learning and portfolio strategies

---

Documents

NOTA BENE: All documents are copyrighted, cannot be copied, printed or ditributed in any way without prior WRITTEN consent from the author

Chapter name	Theoretical part	Implémentation	Results
Classical portfolio management (historical measure)	slides	Python data: CSV format and PICKLE Other data : shorter CSV (30/40) Program: statistical normality tests to fill in Program: statistical normality tests (2023 version) Program: optimal portfolio w/r to random portfolio
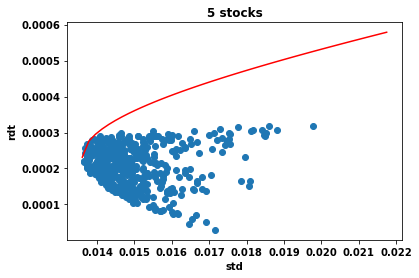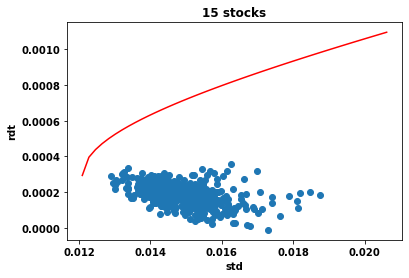
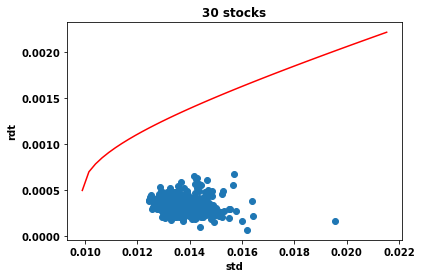Financial derivatives and risk neutral probability	BOOK M1 « Mouvement Brownien et évaluation d’actifs dérivés » slides: reminders for financial derivatives	Code: brownien generation, Euler-Maruyama version to correct + MC computation ; Monte Carlo option price Codes: price & delta of vanilla call and put options, (log-normal = Black-Scholes) model Code delta hedging, Bachelier model version
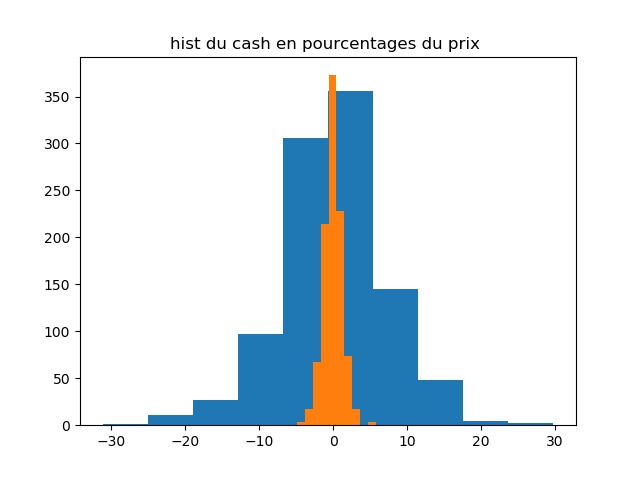Volatility trading	pdf document	Code: vol trading (another version here)	Results
Portfolio insurance: stop-loss, options, CPPIs, Constant Mix	slides, lsections 6.2 of M1 course textbook Written notes Youtube CPPI video: part 1/2, part 2/2 Beta slippage: presentation.	Code: stop loss, CPPI, CPPI v2 Constant-Mix dataC40	Result stop-loss, CPPI, constant-mix
Deep learning for option pricing		Code to fill in: — python notebook or — pure python(rename *.txt to *.py) Corrected code : python notebook
Tools	code exemple: download Yahoo! Finance data
Misc:	Projet (old version)

Historical note: 2019/21 course name: « Approches déterministes et stochastiques pour la valuation d’options »