Auteur : gabriel

« Transformer for Time Series: An Application to the S&P500 » at FICC 2025

gabriel

This joint work with Pierre Brugière has been presented at the at the 8th Future of Information and Communication Conference 2025 held in Berlin, 28-29 April 2025.

Talk materials:

Abstract : The transformer models have been extensively used with good results in a wide area of machine learning applications including Large Language Models and image generation. Here, we inquire on the applicability of this approach to financial time series. We first describe the dataset construction for two prototypical situations: a mean reverting synthetic Ornstein-Uhlenbeck process on one hand and real S&P500 data on the other hand. Then, we present in detail the proposed Transformer architecture and finally we discuss some encouraging results. For the synthetic data we predict rather accuratly the next move, and for the S&P500 we get some interesting results related to quadratic variation and volatility prediction.

Statistics and dynamics of financial derivatives, M2 ISF App, 2020+

gabriel

Teacher: Gabriel TURINICI

Content

  • classical portfolio mangement under historical probability measure: optimal portfolio, arbitrage, APT, beta
  • Financial derivatives valuation and risk neutral probability measure
  • Volatility trading
  • Portfolio insurance: stop-loss, options, CPPI, Constant-Mix
  • Hidden or exotic options: EFT, shorts
  • Deep learning and portfolio strategies

Documents

NOTA BENE: All documents are copyrighted, cannot be copied, printed or ditributed in any way without prior WRITTEN consent from the author

Chapter nameTheoretical partImplémentationResults
Classical portfolio management
(historical measure)		slidesPython data: CSV format and PICKLE
Other data : shorter CSV (30/40)
Program: statistical normality tests to fill in
Program: optimal portfolio w/r to random portfolio, backtest to fill in
Full program: here		optimalCAC40 30_p5optimalCAC40 30_p15
optimalCAC40 30_p30
Financial derivatives and risk neutral probabilityBOOK M1 « Mouvement
Brownien et évaluation d’actifs dérivés »
slides: reminders for financial derivatives		Code: Brownian and log-normal scenario generation,
Euler-Maruyama version to correct + MC computation ;
Monte Carlo option price
Codes: price & delta of vanilla call and put options, (log-normal = Black-Scholes) model
Delta hedging : initial code (notebook or python), final version (notebook or python) Bachelier model version
Volatility tradingpdf documentCode: vol trading (another version here)Results
Portfolio insurance:
stop-loss, options,
CPPIs, Constant Mix		slides,
lsections 6.2 of M1 course textbook
Written notes
Youtube CPPI video:
part 1/2, part 2/2
Beta slippage: presentation.		Code: stop loss, CPPI, CPPI v2
Constant-Mix
dataC40		Result stop-loss, CPPI,
constant-mix
Deep learning for option pricingCode to fill in:
— python notebook
or
— pure python(rename *.txt to *.py)
Corrected code : python notebook
Toolscode
exemple: download Yahoo! Finance data
Misc:Projet (old version)

Historical note: 2019/21 course name: « Approches déterministes et stochastiques pour la valuation d’options » + .

Statistical Learning, M1 Math 2024+

gabriel

Instructor: Gabriel TURINICI

Preamble: this course is just but an introduction, in a limited amount of time, to Statistical and Machine learning. This will prepare for the next year’s courses (some of them on my www page cf. « Deep Learning » and « Reinforcement Learning »).


1/ Introduction to statistical learning : supervised, non-supervised and reinforcement learning, general learning procedure, model evaluation, under and overfitting

2/ K-nearest neighbors and the « curse of the dimensionality »

3/ Regression in high dimensions, variable selection and model regularization (ridge, lasso)

4/ Stochastic gradient descent, mini-batch

5/ Neural networks: introduction, operator, datasets, training, examples, implementations

6/ K-means clustering

Main document for the theoretical presentations: (no distribution autoried without WRITTEN consent from the author): see your « teams » group.

Exercices, implementations: see « teams » group.

Analyse numérique: évolution (M1 Math, Université Paris Dauphine – PSL, 2005-11, 2019-2025

gabriel

Responsable de cours: Gabriel TURINICI
Contenu:
1 Introduction
2 EDO
3 Calcul de dérivée et contrôle
4 EDS
Bibliographie: poly distribué

Documents de support de cours, autres documents

NOTA BENE: Tous des documents sont soumis au droit d’auteur, et ne peuvent pas être distribués sauf accord préalable ÉCRIT de l’auteur.

Supports de cours: livre en anglais « Numerical simulations of time-dependent problems : applied to epidemiology, artificial intelligence and finance »

Implementations TP:

EDO: exo sur la précision, exo stabilité , SIR(EE+H+RK4),  order for the EE/H schemes/SIR

SIR (version controle, adjoint / backward); (version 2023 here)

EDS version 2025 : implémenter : 

1/ simulation brownien

2/ calcul intégrale de W par/rapport à W

3/ calcul par Euler-Maruyama pour équation d’Ornstein-Uhlenbeck

4/ calcul par Euler-Maruyama faible pour modèle log-normal (Black-Scholes)

Version anciennes

2022/23:

2020/21:

« Convergence of a L2 regularized Policy Gradient Algorithm for the Multi Armed Bandit » at ICPR 2024

gabriel

This joint work with Stefana-Lucia ANITA has been presented at the at the 27th International Conference on Pattern Recognition (ICPR) 2024 held in Kolkata, India, Dec 1st through 5th 2024.

Talk materials:

Abstract : Although Multi Armed Bandit (MAB) on one hand and the policy gradient approach on the other hand are among the most used frameworks of Reinforcement Learning, the theoretical properties of the policy gradient algorithm used for MAB have not been given enough attention. We investigate in this work the convergence of such a procedure for the situation when a L2 regularization term is present jointly with the ‘softmax’ parametrization. We prove convergence under appropriate technical hypotheses and test numerically the procedure including situations beyond the theoretical setting. The tests show that a time dependent regularized procedure can improve over the canonical approach especially when the initial guess is far from the solution. 

« Optimal time sampling in physics-informed neural networks » at ICPR 2024

gabriel

This talk has been presented at the at the 27th International Conference on Pattern Recognition (ICPR) 2024 held in Kolkata, India, Dec 1st through 5th 2024.

Talk materials:

Abtract : Physics-informed neural networks (PINN) is a extremely powerful paradigm used to solve equations encountered in scientific computing applications. An important part of the procedure is the minimization of the equation residual which includes, when the equation is time-dependent, a time sampling. It was argued in the literature that the sampling need not be uniform but should overweight initial time instants, but no rigorous explanation was provided for this choice. In the present work we take some prototypical examples and, under standard hypothesis concerning the neural network convergence, we show that the optimal time sampling follows a (truncated) exponential distribution. In particular we explain when is best to use uniform time sampling and when one should not. The findings are illustrated with numerical examples on linear equation, Burgers’ equation and the Lorenz system.

Deep Learning course, 2nd year of Master (ISF App : 2019-25, MATH : 2023-25)

gabriel

Teacher: Gabriel TURINICI


Summary:
1/ Deep learning : major applications, references, culture
2/ Types: supervised, renforcement, unsupervised
3/ Neural networks: main objects: neurons, operations, loss fonction, optimization, architecture
4/ Stochastic optimization algorithms and convergence proof for SGD
5/ Gradient computation by « back-propagation »
6/ Pure Python implementation of a fully connected sequential network
7/ Convolutional networks (CNN) : filters, layers, architectures. 
8/ Keras implementation of a CNN.
9/ Techniques: regularization, hyper-parameters, particular networks, recurrent (RNN, LSTM); 
10/ Unsupervised Deep learning:  generative AI, GAN, VAE, Stable diffusion.
11/ Keras VAE implementation. “Hugginface” Stable Diffusion.
(12/ If time allows: LLM & NLP: word2vec, Glove (exemples : woman-man + king = queen)

Documents
MAIN document (theory): see your teams channel
(no distribution is authorized without WRITTEN consent from the author)		for back-propagationSGD convergence proof
Implementations
Function approximation by NN : notebook version, Python version
Results (approximation & convergence)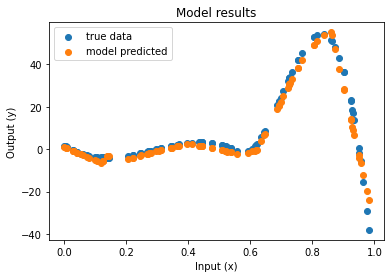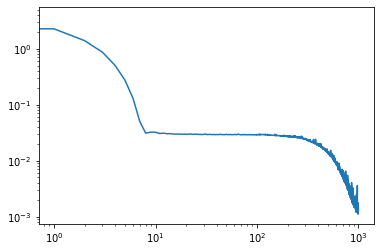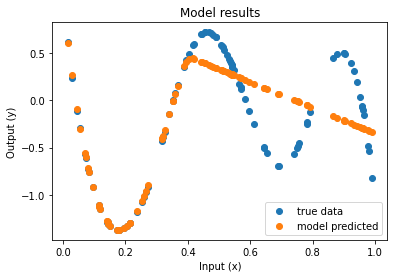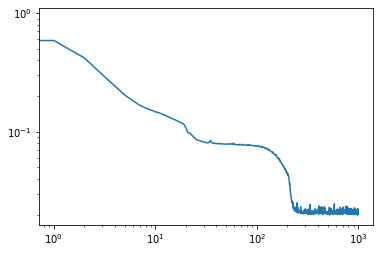

After 5 times more epochs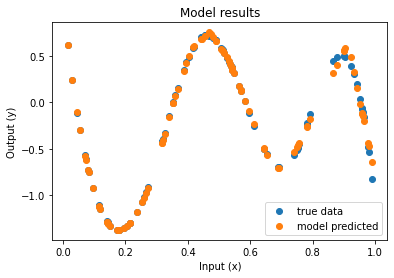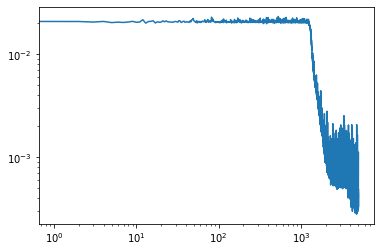
Official code reference https://doi.org/10.5281/zenodo.7220367
Pure python (no keras, no tensorflow, no Pytorch) implementation (cf. also theoretical doc):
– version « to implement » (with Dense/FC layers) (bd=iris),
– version : solution

If needed: iris dataset here
Implementation : keras/Iris

CNN example: https://www.tensorflow.org/tutorials/images/cnn

Todo : use on MNIST, try to obtain high accuracy on MNIST, CIFAR10.
VAE: latent space visualisation : CVAE – python (rename *.py) , CVAE ipynb version
Stable diffusion:

Working example jan 2025: python version, Notebook version

Old working example 19/1/2024 on Google collab: version : notebook, (here python, rename *.py). ATTENTION the run takes 10 minutes (first time) then is somehow faster (just change the prompt text).

General chair of the conference FAAI24 « Foundations and applications of artificial intelligence », Iasi, October 28-30, 2024

gabriel

General chair with C. Lefter and A. Zalinescu of the conference FAAI24 « Foundations and applications of artificial intelligence » Iasi Oct 28-30 2024. At the conference I also serve as tutorial presenter.

LLM and time series at the « 6th J.P. Morgan Global Machine Learning Conference », Paris, Oct 18th, 2024

gabriel

Invited joint talk « Using LLMs techniques for time series prediction » with Pierre Brugiere presented at the 6th JP Morgan Global Machine Learning conference held in Paris, Oct 18th 2024

Talk materials: slides(click here) and here a link to the associated paper.